大気中CO2濃度の上昇の主因は自然現象③
CO2循環モデルの構築
前回検討したように、現在、世界標準とされている「人為的CO2蓄積モデル」は人為的なCO2放出が大気中CO2濃度上昇の原因であるという前提で創造された、自然現象の実体を全く無視した、辻褄合わせのモデルです。今回は、自然現象としての実態に即した形の大気中CO2濃度モデルを構築することにします。
最も基本的な条件は、海洋・地表面環境からのCO2放出源は様々ですが、大気中にCO2が放出されると同時に、大気中に既に存在していたCO2と混合するため、大気中に存在するCO2の挙動は放出された時期、あるいは放出源ごとに分離して考えることは出来ないということです。
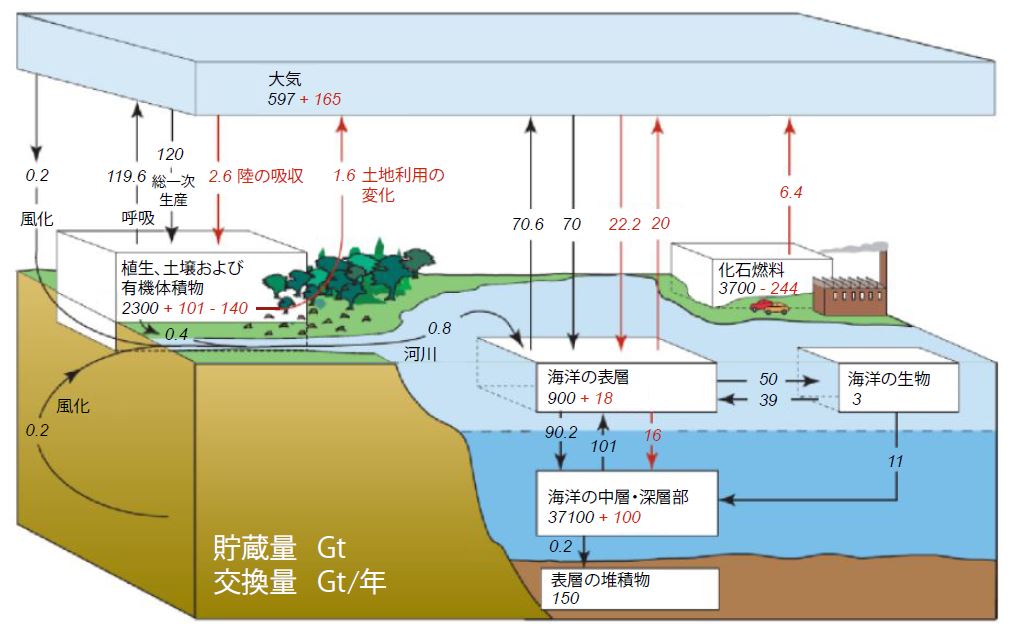
海洋・地表面環境からの主要なCO2放出源は、陸上生態系の呼吸と海洋からの放出です。大気中に存在するCO2の主要な吸収機構は陸上生態系の光合成と海洋の吸収です。
海洋と大気との間のCO2交換は、「温暖化の虚像」2-5節「高校化学で考える化学平衡と大気中CO2濃度」(p.30)で示したCO2の水への溶解反応という可逆反応に従います。したがって、海洋へのCO2の溶解速度は大気中のCO2濃度ないしCO2量Qに比例します。化学平衡状態では海洋からのCO2放出速度と大気から海洋へのCO2溶解速度(吸収速度)は等しくなります。
陸上生態系と大気とのCO2の交換は生態系の呼吸によるCO2放出と、光合成生物によるCO2吸収によっています。陸上生態系の第一生産者である植物を中心とする光合成生物の生産性が陸上生態系の活性度を表すと考えられます。
現在の大気中CO2濃度は光合成生物にとって十分高くはないため、大気中CO2濃度の上昇は光合成生物の生産性を高めます(例えばハウス栽培では施設内のCO2濃度を高くすることで収量の増加を図っています。)。したがって、大気中CO2濃度が上昇することによって、光合成生物のCO2吸収量は増加します。第一次近似として、光合成によるCO2吸収速度は大気中CO2濃度ないしCO2量Qに比例すると考えることができます。
それでも、陸上生態系の大気中CO2濃度変化に対する応答は、植物や動物の成長速度などによる制約からそれほど速くありません。また、化石燃料の燃焼や風化や地表面環境の改変等によるCO2放出は大気中CO2濃度には直接関連付けることは出来ません。
しかし、これらのCO2の放出・吸収の不平衡量は、CO2の水への溶解反応における大気中CO2濃度ないしCO2量Qを変化させた場合に相当するため、海洋のCO2放出・吸収の調整能力によって、速やかに平衡状態を回復します。こうして、化石燃料の燃焼や風化や地表面環境の改変等によるCO2放出は、海洋の調整能力を介して、間接的に大気中のCO2濃度ないしCO2量Qと関連付けられています。
大気中CO2濃度の変化速度は十分小さいので、全体として海洋・地表面からのCO2放出量と大気からのCO2吸収量は等しいと考えて差し支えありません。したがって、人為的CO2蓄積モデルが主張するように、海洋・地表面からのCO2放出量と大気からのCO2吸収量の差が長期間にわたって人為的なCO2放出量の半量程度で変化しないという状況は起こり得ないのです。
以上の条件で、大気中のCO2量のモデルを構成することにします。
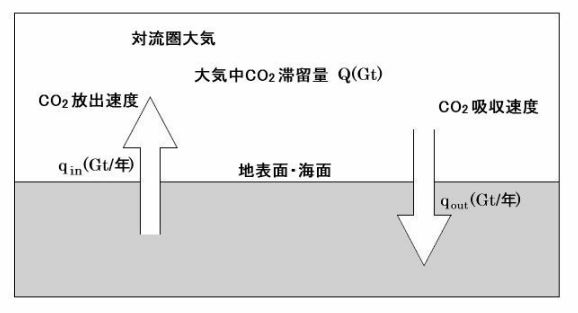
大気中のCO2量Qに関連する構成要素は、海洋・地表面からのCO2放出速度qinと大気からのCO2吸収速度qoutです。
大気中のCO2量Qを定常状態に調整する機構は、大気からのCO2吸収速度qoutがQに比例することです。比例定数(=吸収率)をrとすると、qin = r×Q です。
ある短い時間⊿tに対する大気中のCO2量Qの増分を⊿Qとすると次の関係が得られます。
⊿Q = (qin – qout)×⊿t
この関係は、実は、前回紹介した人為的CO2蓄積モデルの基礎となる式と全く同じです。問題はこの基礎式をどのように展開するか、なのです。前後しますが、ここで再び人為的CO2蓄積モデルについて触れておきます。前回示したように、人為的CO2蓄積モデルでは、
(qin – qout) = 0.5×qinH = 一定
としました。上式を基礎式に適用して⊿t→0の極限を求めると、
dQ = (0.5×qinH) dt
上式の両辺を積分することで人為的CO2蓄積モデルの大気中CO2量Q(t)を求めることができます。
Q(t) = ∫(0.5×qinH)dt = Q0 + 0.5×qinH×t (Q0は積分定数あるいはQの初期値)
これは時間tについての一次関数ですから、時間経過とともに単調に増加し、発散します。また、海洋・地表面からの自然起源のCO2放出qinNの影響を全く表現することができません。つまり、自然起源のCO2放出は大気中CO2量に全く影響しないことを主張しています。したがって、このモデルでは人為的なCO2放出のない場合の大気中CO2量Qは不変であることを主張しているのです。
これは産業革命以前の大気中CO2量の変動を説明することができません。また、人為的CO2蓄積モデルは将来的に人為的なCO2放出をゼロにしても大気中のCO2量は一切減らすことができないことをも主張しているのです。
話を基に戻します。循環モデルでは、
⊿Q = (qin – qout)×⊿t = (qin – r×Q)×⊿t
⊿Q/⊿t = qin – r×Q
この式について、⊿t→0の極限を求めることで、Qの時間に対する変化率を表す微分方程式を求めることができます。
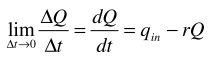
この微分方程式に対して、二つの解を求めることにします。大気中CO2量Qの変化は十分遅いため、大気中のCO2の静的な性質を考察する場合には、近似的に微分方程式の定常解(時間に対する依存性のない解、平衡状態を示す解。)を使うことができます。
定常解は、微分方程式においてdQ/dt = 0とすることによって求めることができます。
0 = qin – rQ ∴Q = qin/r, qin = qout
時間に対する変化を調べる場合には微分方程式の一般解を求める必要があります。qin、rが時間に依存する場合には、一般解を解析的に求めることができるとは限りません(数値的な解析手段を用いることになります。)。ここでは解析解が求められる最も簡単な場合として、qin = 一定かつr = 一定という条件の下での一般解を示しておきます。
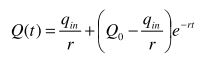
この解は、大気中CO2量がQ0 = 一定という定常状態に対して、qinに有限の変化が生じた場合のQの時間に対する変化を表すことができます。右辺第一項は定数であり、第二項は時間経過に伴って急速に0に収束します。つまりQ(t)は時間経過とともに急速に右辺第一項で示される新しい定常状態に収束することになります。
ここで、IPCC2007年報告の産業革命以前の定常状態(qin=190.2Gt/年=qout、r=190.2/597=0.3186)に対して、ステップ関数的に人為的なCO2放出6.4Gt/年が増加した場合についてシミュレーションした結果を示します。
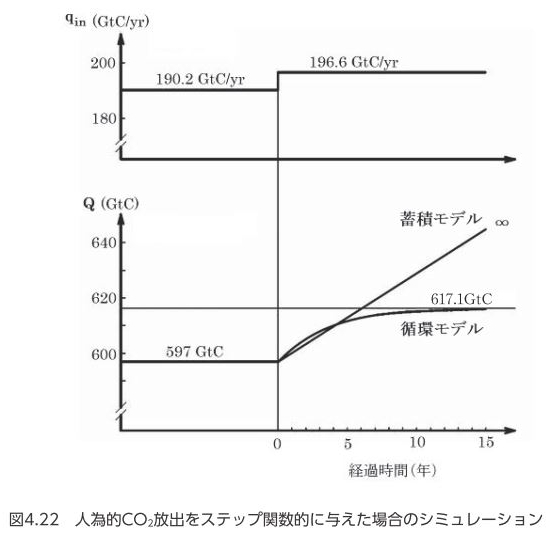
上図にはCO2循環モデルと参考のために人為的CO2蓄積モデルによる大気中CO2量Qの時間tに対する変化を示しています。循環モデルではわずか15年間程度で定常値に収束しますが、人為的CO2蓄積モデルでは発散することがわかります。
実際には人為的なCO2放出量qinは産業革命以後200年間程度をかけてゆっくり6.4Gt/年にまで増加しました。したがって、この間、常にqin ≒ qoutであったと考えてよいでしょう。
図4.22に示した一般解を用いたシミュレーションでは、実際には産業革命以降200年余りかけて6.4Gt/年に増加したqinHを一瞬で増加させた場合について示しました。例えばこれを、20年毎に0.64Gt/年づつ増加したとすると、次のようになります。
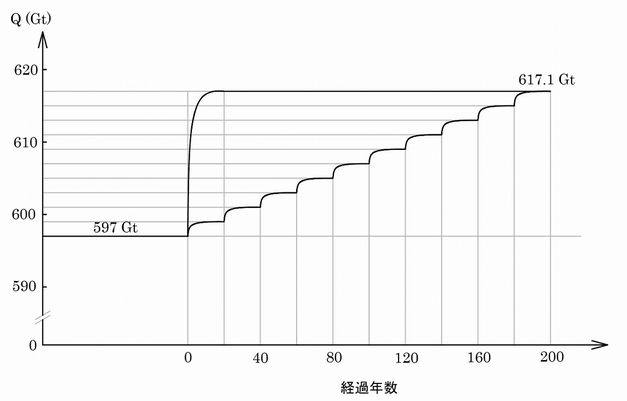
上図には比較のために一度に6.4Gt/年を与えた場合も示しています。一度に6.4Gt/年を増加させた場合、最大でqinとqoutの差は6.4Gt/年です。これを20年毎に0.64Gt/年づつ増加させると、各期首に最大でqinとqoutの差は0.64Gt/年になります。
理論的には、期間の分割数を無限大にした場合の極限がqinが連続的に変化した場合を表すことになります。
分割数→∞ のとき (qin - pout ) → 0 つまり qin ≒ qout
と考えてよいでしょう。緩やかで連続的な入力の変化に対しては、入力と出力は等しいと考えて差し支えないでしょう。
したがって、人為的CO2蓄積モデルが主張するように、qinとqoutの差が6.4Gt/年の半分の3.2Gt/年よりも小さくならないという主張はあり得ないのです。
